三维模型的表示方法
- 点云:
- 点云是在同一空间参考系下表达目标空间分布和目标表面特性的海量点集合。
- 结合激光测量和摄影测量原理得到点云,包括三维坐标(XYZ)、激光反射强度(Intensity)和颜色信息(RGB)。
- 在获取物体表面每个采样点的空间坐标后,得到的是一个点的集合,称之为"点云"。
- 网格(mesh):
- 多边形网格(Polygon mesh)是三维计算机图形学中表示多面体形状的顶点与多边形的集合,它也叫作非结构网格。
- 这些网格通常由三角形、四边形或者其它的简单凸多边形组成,这样可以简化渲染过程。但是,网格也可以包括带有空洞的普通多边形组成的物体。
- 体素(voxel):
- 体素是体积像素(volume pixel)的简称。
- 如同像素,体素本身并不含有空间中位置的数据即(它们的坐标),却可以从它们相对于其它体素的位置来推敲,意即它们在构成单一张体积影像的数据结构中的位置。
- 深度图:
- 深度图像也被称为距离影像,是指将从图像采集器到场景中各点的距离(深度)作为像素值的图像,它直接反映了景物可见表面的几何形状。
- 深度图像经过坐标转换可以计算为点云数据,有规则及必要信息的点云数据也可以反算为深度图像数据。
- 深度值的大小只与距离有关,而与环境、光线、方向等因素无关。
三维重建比较常见的流程
- 提取图像特征(SIFT、SURF等)-->利用特征计算图像之间的特征匹配-->基于匹配的特征进行稀疏重建,得到各个图像的相机位姿和稀疏的特征点云(SFM)-->基于相机位姿进行稠密重建,得到稠密点云(PMVS/CMVS)-->基于点云重建网格、体素或者纹理
三维重建技术方法
- 三维重建技术的重点在于如何获取目标场景或物体的深度信息。在景物深度信息已知的条件下,只需要经过点云数据的配准及融合,即可实现景物的三维重建。
- 人们按照被动式测量与主动式测量对目标物体深度信息的获取方法进行了分类:
被动式三维重建技术
- 被动式一般利用周围环境如自然光的反射,使用相机获取图像,然后通过特定算法计算得到物体的立体空间信息。主要有以下三种方法:
- 纹理恢复形状法
- 作为图像视野中不断重复的视觉基元,纹理元覆盖在各个位置和方向上。当某个布满纹理元的物体被投射在平面上时,其相应的纹理元也会发生弯折与变化。
- 例如透视收缩变形使与图像平面夹角越小的纹理元越长,投影变形会使离图像平面越近的纹理元越大。通过对图像的测量来获取变形,进而根据变形后的纹理元,逆向计算出深度数据。
- 阴影恢复形状法
- 图像的阴影边界包含了图像的轮廓特征信息,因此能够利用不同光照条件下的图像的明暗程度与阴影来计算物体表面的深度信息,并以反射光照模型进行三维重建。
- 立体视觉法(MVS)
- 主要包括直接利用测距器获取程距信息、通过一幅图像推测三维信息和利用不同视点上的两幅或多幅图像恢复三维信息等三种方式。
主动式三维重建技术
- 主动式是指利用如激光、声波、电磁波等光源或能量源发射至目标物体,通过接收返回的光波来获取物体的深度信息。
- 飞行时间法(ToF)
- 通过测量发射信号与接收信号的飞行时间间隔来获得距离的方法。
- 结构光法
- 结构光是将已知图案(通常是栅格或水平条)投射到场景上的过程。这些物体在撞击表面时变形的信息来在视觉系统中计算场景中物体的深度和表面信息,用投影仪投射特定的光信息到物体表面后及背景后,由摄像头采集。根据物体造成的光信号的变化来计算物体的位置和深度等信息,进而复原整个三维空间。
- 首先利用激光投影仪向目标物体投射可编码的光束,生成特征点;然后根据投射模式与投射光的几何图案,通过三角测量原理计算摄像机光心与特征点之间的距离,由此便可获取生成特征点的深度信息,实现模型重建。这种可编码的光束就是结构光。
- 三角测距法
- 红外设备以一定的角度向物体投射红外线,光遇到物体后发生反射并被CCD图像传感器所检测。随着目标物体的移动,此时获取的反射光线也会产生相应的偏移值。根据发射角度、偏移距离、中心矩值和位置关系,便能计算出发射器到物体之间的距离。
基于Kinect深度图的三维重建
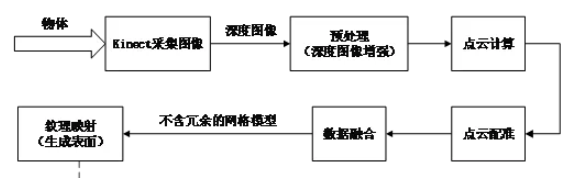
对获取到的每一帧深度图像均进行前六步操作,直到处理完若干帧,最后完成纹理映射。
深度图像获取
预处理
- 对图像进行去噪和修复等图像增强过程。
点云计算
- 相机标定之后,利用相机的内外参数矩阵获得从图像坐标系到世界坐标系的映射。
点云配准
点云配准过程,就是求一个两个点云之间的旋转平移矩阵(rigid transform or euclidean transform 刚性变换或欧式变换),将源点云(source cloud)变换到目标点云(target cloud)相同的坐标系下。
可以表示为以下方程:
\[ p_{t} = R\cdot p_{s} \ + \ T \]
其中 \(p_{t}, \ p_{s}\) 就是target cloud与source cloud中的一对对应点。
而我们要求的就是其中的R与T旋转平移矩阵。
这里,我们并不知道两个点集中点的对应关系。这也就是配准的核心问题。
粗配准
ICP算法的基本原理。它需要一个旋转平移矩阵的初值。这个初值如果不太正确,那么由于它的greedy优化的策略,会使其目标函数下降到某一个局部最优点(当然也是一个错误的旋转平移矩阵)。因此,我们需要找到一个比较准确的初值,这也就是粗配准需要做的。
评价标准:比较通用的一个是LCP(Largetst Common Pointset)。给定两个点集P,Q,找到一个变换T(P),使得变换后的P与Q的重叠度最大。在变换后的P内任意一点,如果在容差范围内有另外一个Q的点,则认为该点是重合点。
精配准
- 精配准就是在已知一个旋转平移的初值的情况下(这个初值大概已经是正确的了),进一步计算得到更加精确的旋转平移矩阵。
- 精配准的模式基本上已经固定为使用ICP算法(Iterative Closest Point)及其各种变种。
- 简要介绍一下点集到点集ICP配准的算法:
- ICP算法核心是最小化一个目标函数
\[ f(R,T) = \frac{1}{N_{p}} \sum_{i=1}^{n}|p_{t}^i-R\cdot p_{s}^i-T|^2 \]
\(p_{t}^i,\ p_{s}^i\) 就是一对对应点,总共有\(N_{p}\) 对对应点。这个目标函数实际上就是所有对应点之间的欧式距离的平方和。
- 寻找对应点
我们现在并不知道有哪些对应点。因此,我们在有初值的情况下,假设用初始的旋转平移矩阵对source cloud进行变换,得到的一个变换后的点云。然后将这个变换后的点云与target cloud进行比较,只要两个点云中存在距离小于一定阈值(ICP中的一个参数),我们就认为这两个点就是对应点。这也是"最邻近点"这个说法的来源。
- R、T优化
有了对应点之后,我们就可以用对应点对旋转R与平移T进行估计。这里R和T中只有6个自由度,而我们的对应点数量是庞大的(存在多余观测值)。因此,我们可以采用最小二乘等方法求解最优的旋转平移矩阵,就是让R和T去拟合大多数的对应点。
- 迭代
我们优化得到了一个新的R与T,导致了一些点转换后的位置发生变化,一些最邻近点对也相应的发生了变化。因此,我们又回到了步骤2)中的寻找最邻近点方法。2)3)步骤不停迭代进行,直到满足一些迭代终止条件,如R、T的变化量小于一定值,或者上述目标函数的变化小于一定值,或者邻近点对不再变化等。(ICP算法中的一个参数)
- 算法大致流程就是上面这样。这里的优化过程是一个贪心的策略。首先固定R跟T利用最邻近算法找到最优的点对,然后固定最优的点对来优化R和T,依次反复迭代进行。这两个步骤都使得目标函数值下降,所以ICP算法总是收敛的,这也就是原文中收敛性的证明过程。这种优化思想与K均值聚类的优化思想非常相似,固定类中心优化每个点的类别,固定每个点的类别优化类中心。
全局配准
全局配准是使用整幅图像直接计算转换矩阵。通过对两帧精细配准结果,按照一定的顺序或一次性的进行多帧图像的配准。这两种配准方式分别称为序列配准(Sequential Registration)和同步配准(Simultaneous Registration)。
配准过程中,匹配误差被均匀的分散到各个视角的多帧图像中,达到削减多次迭代引起的累积误差的效果。值得注意的是,虽然全局配准可以减小误差,但是其消耗了较大的内存存储空间,大幅度提升了算法的时间复杂度。
数据融合
经过配准后的深度信息仍为空间中散乱无序的点云数据,仅能展现景物的部分信息。因此必须对点云数据进行融合处理,以获得更加精细的重建模型。以Kinect传感器的初始位置为原点构造体积网格,网格把点云空间分割成极多的细小立方体,这种立方体叫做体素(Voxel)。通过为所有体素赋予SDF(Signed Distance Field,有效距离场)值,来隐式的模拟表面。
SDF值等于此体素到重建表面的最小距离值。当SDF值大于零,表示该体素在表面前;当SDF小于零时,表示该体素在表面后;当SDF值越接近于零,表示该体素越贴近于场景的真实表面。KinectFusion技术虽然对场景的重建具有高效实时的性能,但是其可重建的空间范围却较小,主要体现在消耗了极大的空间用来存取数目繁多的体素。
为了解决体素占用大量空间的问题,Curless等人提出了TSDF (Truncated Signed Distance Field,截断符号距离场)算法,该方法只存储距真实表面较近的数层体素,而非所有体素。因此能够大幅降低KinectFusion的内存消耗,减少模型冗余点。
表面生成
表面生成的目的是为了构造物体的可视等值面,常用体素级方法直接处理原始灰度体数据。Lorensen提出了经典体素级重建算法:MC(Marching Cube,移动立方体)法。移动立方体法首先将数据场中八个位置相邻的数据分别存放在一个四面体体元的八个顶点处。对于一个边界体素上一条棱边的两个端点而言,当其值一个大于给定的常数T,另一个小于T时,则这条棱边上一定有等值面的一个顶点。
然后计算该体元中十二条棱和等值面的交点,并构造体元中的三角面片,所有的三角面片把体元分成了等值面内与等值面外两块区域。最后连接此数据场中的所有体元的三角面片,构成等值面。合并所有立方体的等值面便可生成完整的三维表面。